北京大学物理学院量子材料科学中心陈昱安助理教授及其博士生梁子健，联合中国科学技术大学国家同步辐射实验室副研究员刘科、中国科学院理论物理研究所副研究员宋昊等合作者，近日在量子纠错与拓扑量子码研究中取得重要进展。研究团队提出了一种基于环论的代数几何方法，能够高效分析二维拓扑 CSS 纠错码，并在扭曲环面上构建出一系列具有更大逻辑维度和更优局域性的广义环面码（generalized toric codes）。相关成果以“扭曲广义环面码用于量子纠错”（Generalized Toric Codes on Twisted Tori for Quantum Error Correction）和 “高效率量子低密度奇偶校验码的任意子理论与拓扑阻挫”（Anyon Theory and Topological Frustration of High Efficiency Quantum Low-Density Parity-Check Codes）为题发表在国际期刊 PRX Quantum 和 Physical Review Letters。

实现大规模容错量子计算的过程中，量子纠错是不可或缺的核心环节。理想的量子比特极易受到环境噪声干扰，如果缺乏有效保护，量子信息将在极短时间内退相干并迅速丢失。拓扑量子码因其稳固的抗局域扰动能力而成为研究热点，其中Kitaev环面码（toric code）是最具代表性的方案。它具有局域稳定子和高阈值等优势，已在理论和实验中得到广泛研究。然而，传统环面码、环面码的逻辑维度不随系统规模增长，若要获得多个逻辑比特，往往需要通过打孔或码手术（code surgery）等方式扩展晶格，导致码距降低、整体资源开销巨大。为了克服这一局限，近年来低密度奇偶校验量子（qLDPC）码迅速发展，被认为是兼顾编码率与可实现性的有力候选。如何在保持低权重稳定子和局域性的前提下，同时提升逻辑比特数与码距，已成为当前量子纠错理论与实验的核心挑战。因此，亟需一种统一而高效的分析框架，能够在有限尺寸与一般化边界条件下，准确刻画拓扑量子码的逻辑维度、任意子结构与实现复杂度，并为优参数族的系统性探索提供理论依据。

文章所用广义环面码的稳定子形式如图1所示。相同的稳定子实现在不同晶格上会得到不同的qLDPC码。图2展示了扭曲环面的几何结构及其二维投影。扭曲环面的主要优势在于能够显著提升码距，并在保持局域稳定子的同时实现更优的 [[n,k,d]] 纠错码。例如，在 [[360,12,≤24]] 的构造中，稳定子的远程作用由 IBM 方案 [Nature 627, 778 (2024)] 的 9 降低至 3，大幅改善了实验可实现性。

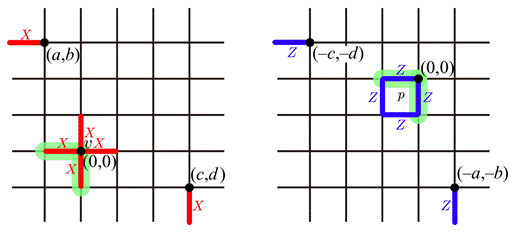
图1：广义环面码的Av和Bp稳定子由多项式的参数化。

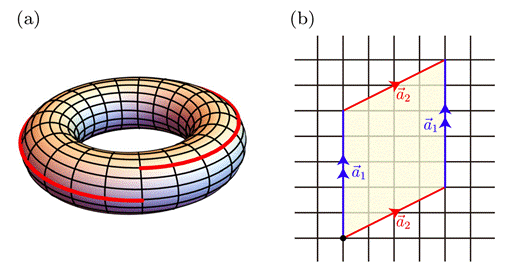
图2：(a)嵌入在三维空间中的扭曲环面。环面沿其纵向方向按2π的分数进行扭转，红色曲线标示的大回路体现了这一特征。(b)扭曲环面的二维投影图，其中将向量 a1 和 a2 的端点视为同一点，并将平行四边形的对边粘合，从而形成扭曲环面的拓扑结构。

研究围绕二维拓扑CSS码，能够直接从任意子结构解析出逻辑维度与逻辑算符，避免了传统方法中对大规模稀疏矩阵秩计算的依赖。借助该方法，研究团队在扭曲环面上系统性地构建并筛选出一系列权重为6、局域性更优的广义环面码，涵盖 [[120,8,12]]、[[210,10,16]]、[[254,14,16]]、[[310,10,≤22]]、[[340,16,18]]、[[360,12,≤24]] 等多组新发现的参数或更具局域性的实现。结果表明，通过边界扭曲可在更小的晶格上实现与常规大环面码相当甚至更优的编码性能。这些成果不仅为拓扑量子码的系统分析与优化提供了普适工具，也为qLDPC码的构造开辟了新路径。尤其在近期实验条件下，该方法能够在保持低权重稳定子的同时提升逻辑比特数和码距，为构建可扩展容错量子计算提供了新的可行方向。

另外，研究融合代数、几何与拓扑方法，建立了分析双变量双循环量子纠错码的理论框架。研究引入“分形子”视角并结合Gröbner基工具，揭示了这类量子码普遍具有拓扑序和类分形子任意子激发的特征。同时，还发现了不同于传统拓扑码的“拓扑阻挫”现象。此外，研究利用Koszul复形和BKK定理等代数几何方法，高效刻画了任意子与逻辑算子之间的关系，并揭示了BB码拓扑序的整体规律。任意子的种类可通过计算由相互作用形式决定的牛顿多面体的混合体积获得（见图3）。这一系列成果不仅深化了量子纠错、任意子激发与对称性拓扑物态之间的联系，也为发展高性能qLDPC码提供了重要理论支撑。

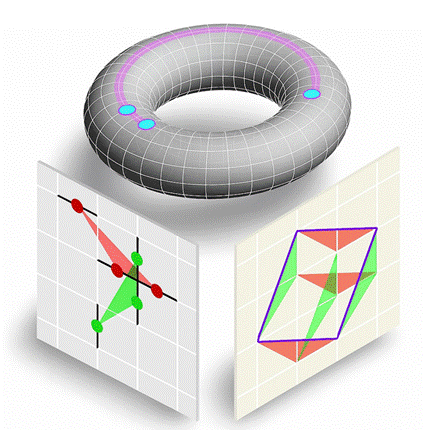
图3：环面上任意子的类分形子移动行为，以及通过牛顿多面体（红色与绿色三角形）的混合体积（紫色平行四边形）计算任意子种数的代数几何方法，其中牛顿多面体由相互作用量子比特的相对位置确定。

该工作[PRX Quantum 6, 020357 (2025)]中，梁子健为第一作者，陈昱安为通讯作者。研究工作得到了国家自然科学基金委员会、北京大学、中国科学院、安徽省和上海市的经费支持。

原文链接：

1. https://doi.org/10.1103/rmy6-9n89

2. https://doi.org/10.1103/86j7-cmsw